Basics of Coordinate Geometry for Class 10 Maths

Coordinate Geometry which is also know as the analytic geometry is one of the most interesting concepts of mathematics. Coordinate Geometry represents the link between geometry and algebra through graphs involving lines and curves.

Points on a Cartesian Plane

The coordinates are a pair of numbers locate points on a plane. There are two terms that is usually to describe the points that are abscissa and ordinates. Abscissa or x-coordinate is the distance of a point from the y-axis. Ordinates or y-coordinate is the distance of a point from the x-axis.

Distance Formula

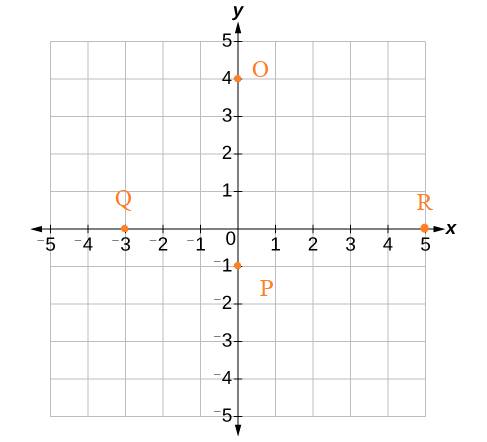
Distance Between Two Points on the Same Coordinate Axes

The difference between on the same plane represent the distance between two points on that plane. For example, if the points are on the y-axis the distance between two points is given by the difference between their ordinates. Similarly, if the points are on the x-axis the difference between their abscissa represent the distance between them.

Distance OP = 4 – (-1) = 5 units

Distance QR = 5 – (-3) = 8 units

Calculating Distance Between Two Points Using Pythagoras Theorem

Pythagoras Theorem is a significant topic in Class 10 Maths, which describes the relation between the sides of a right-angled triangle. It is also sometimes known as the Pythagorean Theorem. Before understanding the formula and the proof of Pythagoras theorem, you need to have some basic knowledge about right angle triangle. Pythagorean theorem states that “The square of the hypotenuse side of an right-angle triangle is equal to the sum of squares of the other two sides of the right-angle triangle “. The sides of this triangle have been termed as Base, Perpendicular, and Hypotenuse. Here, the longest side is known as the hypotenuse, as it is opposite to the angle 90°.

Calculating distance between two points using Pythagoras Theorem

Let B (c, d) and A (a, b) be any two points on the cartesian plane.
Draw lines parallel to the axes through B and A to meet at C.

Δ BCA is right-angled at C.

By Pythagoras Theorem,

BA²     = BC² + AC²

= (a – c)² + (b – d)²

BA = √[a – c)² + (b – d)²]

Now, using distant formula,

Distance between any two points (c, d) and (a, b) is given by
d = √[a – c)²+(b – d)²]
Where d is the distance between the points (c, d) and (a, b).

Section Formula

A(a, b) and B(c, d) internally in the ratio m:n, then, the coordinates of P are given by the section formula as:

P(x, y)=(mc+na/m+n ; md+nb/m+n)

To find the ratio in which a given point P(x, y) divides the line segment joining A(a, b) and B(c, d),

• Assume that the ratio is k : 1
• Substitute the ratio in the section formula for any of the coordinates to get the value of k.

x=kc+a/k+1

When a, c and x are known, k can be calculated. The same can be calculated from the y- coordinate also.

Midpoint

The midpoint of any line segment divides it in the ratio 1 : 1.
The coordinates of the midpoint(P) of line segment joining A(a, b) and B(c, d) is given by

p(x, y)=(a+c2/b+d2)

Points of Trisection

To find the points of trisection P and Q which divides the line segment joining
A(a, b) and B(c, d) into three equal parts:

• i) AP : PB = 1 : 2

P=(c+2a/3; d+2b/3)

• ii) AQ : QB = 2 : 1
  Q=(2c+a/3; 2d+b/3)

Centroid of a triangle

If A(a, b),B(c, d) and C(e, f) are the vertices of a ΔABC, then the coordinates of its centroid(P) is given by
p(x, y)=(a+c+e3,b+d+f3)

Area from Coordinates

Area of a triangle given its vertices

If A(a, b),B(c, d) and C(e, f) are the vertices of a Δ ABC, then its area is given by

A = 1/2[a(d − f) + c(f − b) + e(b − d)]
Where A is the area of the Δ ABC.

To know more about Area of a Triangle,

Collinearity Condition

If three points P, Q and R are collinear and Q lies between P and R, then,

• PQ + QR = PR.  PQ, QR, and PR can be calculated using the distance formula.
• The ratio in which Q divides PR, calculated using section formula for both the x and y coordinates separately will be equal.
• Area of a triangle formed by three collinear points is zero.